 |
Lecture Notes - Week 6
These are protocols that allow two persons to exchange cryptographic keys in order to conduct a private communication.
A key k for symmetric encryption can be exchanged over a secure channel, eg a trusted messenger.
To avoid encrypting a large number of messages with the same key, k can be used as a "master key" which is used once for each session to exchange a new key ks as a session key, eg by establishing a new key ks and sending it to the other party, encrypted as E(ks, k).
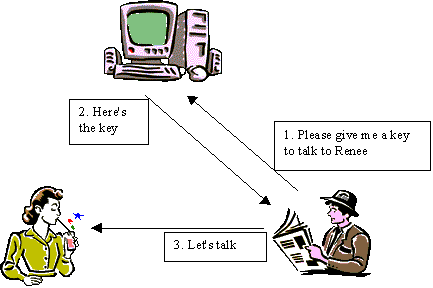
Two users may utilise a central key distribution agency to establish a new
symmetric key for their communication.

Assume that Pablo wishes to communicate with Renee. P shares a symmetric key KP with the agency and R shares a key KR with the agency. See Figure 1.
1. P sends (P, R, IP) to the agency where P and R are the names and IP is P's reference number.
2. The agency sends E((IP, R, KPR, E((KPR, P), KR)), KP) back to P. P checks whether IP and R are corrected. P now has a key KPR to communicate with R and a cryptogram that he can't read.
3. P sends E((KPR, P), KR) to R. R knows that P wants to communicate with her and that KPR is a key that was issued by the agency.
4. P and R now have a shared key KPR to communicate with each other.
Exercise: What possible attacks could be mounted by eavesdropper Octavia? Is the protocol susceptible to any of these attacks?
Given that P has public and private keys EP and
DP and that R has public and private keys ER and DR,
P could send messages directly R using ER. However, since symmetric
encryption is much faster than public-key encryption, P would normally select a
symmetric key KPR to communicate with R and will send that key to R
as ER(KPR). This message could, however, be forged by O.
Therefore P seals the message with his signature and both parties confirm that
they a have a "live" key, ie not a key replayed from a previous
communication. See Figure 2.
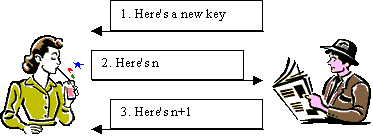
1. P sends ER(DP(KPR)) to R. R can obtains KPR = DR(EP(ER(DP(KPR)))) and is convinced that the message is authentic.
2. R sends E(n, KPR) with a random number n to P.
3. P sends E(f(n), KPR) back to R where f(n) is an agreed function, eg f(n)=n+1.
This protocol works as long as P and R can be sure that they have each other's genuine public keys.
For the secure distribution of public keys an agency can be used. See Figure 3.
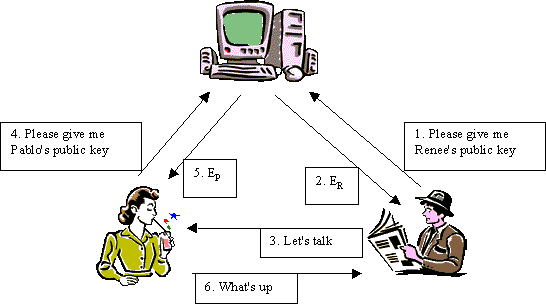 |
1. P sends a message (P, R) to the agency D.
2. D responds with DD((ER, R)) sealing the message with its private key.
3. P decrypts the message with the agency's public key and is sure to have R's public key.
4. P sends a message ER((P, IP)) to R where IP is P's message reference number
5. R sends a message (R, P) to the agency D.
6. D responds with DD((EP, P)) sealing the message with its private key.
7. R decrypts the message with the agency's public key and is sure to have P's public key.
This protocol is secure as long as the agency has indeed the genuine public keys of both parties.
A certificate comprises a person's (or machine's) identity and his/her/its public key, authenticated by the issuer of the certificate, similarly to, for example, a driver's licence linking a person's photograph to his/her name as authenticated by the issuing authority's stamp and signature.
In a hierarchical structure, it is assumed that each
immediate superior knows her immediate subordinates. For example in the company
structure in Figure 4, Diana obtains a certificate as follows:
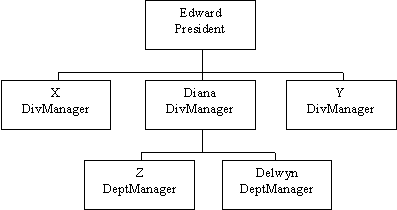
1. Diana creates (Name=Diana, Pos=DivManager, PubKey=17EF83)
2. Edward adds hash and signs: DEd((Name=Diana, Pos=DivManager, PubKey=17EF83CA, Hash= 128C4)) which is Diana's certificate.
Similarly, Delwyn obtains a cerficate as follows:
1. Delwyn creates (Name=Delwyn, Pos=DeptManager, PubKey=3AB3882C)
2. Diana adds hash and signs: DDi((Name= Delwyn, Pos=DeptManager, PubKey=3AB3882C, Hash= 48CFA)), then appends her certificate DEd((Name=Diana, Pos=DivManager, PubKey=17EF83CA, Hash= 128C4)). This is Delwyn 's certificate.
This self-enforcing protocol allows two players to play poker by email. To simplify things, assume that there are 10 cards of which A obtains 5 at random and B obtains 5 at random. Assuming commutative encryption, this is achieved by the following protocol:
1. A encrypts the 10 cards c1 … c10 with her key and sends E(c1, KA) … E(c10, KA) to B.
2. B chooses 5 cards, say c1 … c5, and sends E(c1, KA) … E(c5, KA) back to A.
3. B encrypts the other 5 cards c6 … c10 with his key and sends E(E(c6, KA), KB) … E(E(c10, KA), KB) back to A.
4. A decrypts all 10 cards and has c1 … c5, and E(c6, KB) … E(c10, KB), [assuming that the 2 encryptions are commutative].
5. A sends E(c6, KB) … E(c10, KB) back to B.
6. B decrypts the 5 cards and has c6 … c10.
Exercise: Modify the protocol for a game with 32 cards of which 5 are dealt to each of 2 players.
Normally, users cannot or don't want to generate their own keys and there is legitimate concern that the key distribution agency should not know which key pair it has given to which user. Of course the agency cannot simply let users choose a key pair from a published list because anyone else would have a convenient mapping between public and private keys. A possible solution is derived from the remote poker game:
1. A send out a constant stream of key pairs E((Ei, Di), KA) encrypted with her key KA.
2. B picks one key pair at random, encrypts it with his key KB and sends E(E((Ej, Dj), KA), KB) back to A.
3. A decrypts it with her key KA and sends E((Ej, Dj), KB) back to A.
4. B decrypts it with his key KB and has his key pair (Ej, Dj).
A remote voting protocol needs to fulfil the following criteria:
· Only authorised users can transmit messages.
· Each user can only transmit 1 message.
· It is impossible to determine who sent a particular message.
Assume 3 voters J, K and L, each of whom has a vote v (v=0 or v=1). Each voter has public-key encryption/decryption functions E and D. Each voter also has another public encryption function R which embeds v in a random string and the corresponding decryption function Q. The voting is conducted as follows:
1. Each voter encrypts RJ(RK(RL(EJ(EK(EL(vj)))))) and send it to J. Records are kept of the intermediate encryption results.
2. J verifies that her vote is in the set.
3. J decrypts with QJ, scrambles the order and sends the set of RK(RL(EJ(EK(EL(vi))))) to K.
4. K verifies that his vote is in the set, using his record of the intermediate encryption results.
5. K decrypts with QK, scrambles the order and sends the set of RL(EJ(EK(EL(vi)))) to L.
6. L verifies that her vote is in the set, using her record of the intermediate encryption results.
7. L decrypts with QL, scrambles the order and sends the set of EJ(EK(EL(vi))) to J.
8. L also signs the set and sends the signature to J and K.
9. J decrypts with DJ and sends the set of EK(EL(vi)) to K.
10. J also signs the set and sends the signature to K and L.
11. K decrypts with DK and sends the set of EL(vi) to L.
12. K also signs the set and sends the signature to J and L.
13. L decrypts with DL and publishes the resulting vi.
This protocol works because in steps 1-7, the individual votes are not revealed, but each voter can verify that his/her vote is still in the set. This is due to the embedding in random bit strings. Forgery in steps 8-13 is transparent because everyone can reverse the steps 13, 11 and 9 and thereby confirm that no tampering has taken place. Moreover, if anyone had modified the votes in steps 8-13, the digital signatures in steps 8, 10 and 12 would reveal who had done the tampering.
The problem of sending one of two possible messages such that neither sender nor receiver knows until later which of the two is sent. Example: P and N decide to flip a coin. Heads wins. The following protocol achieves this in a fair manner:
1. P chooses to public-key pairs Ei, Di and Ej, Dj.
2. N chooses a symmetric key KN to a symmetric encryption function S(.).
3. P send Ei and Ej to N.
4. N chooses either i or j, call it h, and sends Eh(KN) to P.
5. P chooses either i or j, suppose it is j, and computes K?=Dj(Eh(KN)). If h=j, then K?=KN, other K? is meaningless.
6. P send S("heads", K?) to N.
7. N decrypts S(S("heads", K?), KN) and either obtains "heads" or a meaningless string.
8. For control, P gives Di and Dj to N who can then verify that h=i or h=j.
The problem of two parties simultaneously signing a contract without a truusted third party requires
· Simultaneous commitment
· Unforgeability
This can be achieved by splitting one's signature into parts (say 4 quarters) and transmitting the parts by oblivious transfer, such that neither party can be aware exactly at which point the signatures have been transmitted in full.
Assume that A and B want to simultaneously sign a contract:
1. Both A and B randomly select 2n symmetric keys (eg DES) and group them in pairs.
2. Both A and B generate n pairs of messages Li and Ri, eg "This is the left half of my signature" and "This is the right half of my signature". The contract is considered signed if either party can produce both halves, Li and Ri, for any i.
3. Both A and B encrypt each message pair with each DES key pair, left half with left key, right half with right key.
4. They send each other the 2n encrypted messages, labelling the messages as c(Li) or c(Ri).
5. A and B send each key pair by oblivious transfer to each other, ie neither knows which of the two keys of a pair has been transmitted.
6. Both A and B decrypt all the messages they can and verify that they are valid.
7.
For b = 1 … keylength
A and B send each other the
bit b of each of the 2n keys
8. A and B decrypt the remaining halves of the messages and the contract is signed.
What if A sent nonsense in steps 4 or 5? B would notice in step 6.
What if A sent only one half of each pair correctly in step 4? She has a 50% chance of getting away with it for each pair. Therefore n should be large, eg for n=10, A's chance of cheating is 1/1024.
What if A stops sending bits in the loop in step 7 and determines the rest of the key by brute force? At that point B has the same chance of determine the rest of the key by brute force (given the same computing power).
What if A sends identical messages in step 5? B will notice this from the record of the protocol.
Similar protocols allow the sending of certified mail, message against receipt, and the simultaneous exchange of secrets. See B. Schneier, Applied Cryptography, ss 5.8 and 5.9).
Note that a lost keys presents a problem in authentication protocols: a user who wants to repudiate a digital signature, for example, may state that the private key was revealed before the transaction took place.
Block ciphers, eg the 64-bit DES scheme, will encrypt identical 8-byte blocks identically. For example, a bank transfer may be transmitted in a 40-byte message as follows:
|
Account Name (24 bytes) |
Acct No (8) |
Xfer Amt (8) |
Since this message makes up 5 DES data blocks, single blocks can be intercepted and replayed in the context of other messages, eg changing the transfer amount in another message. This can be avoided using Block Chaining where a sequence of blocks B1, B2, B3 etc is transmitted as C1, C2, C3 etc with C1=B1, C2=C1+B2, C3=C2+B3 where the + is an exclusive-or operation.